Analysing the impact of max_dept parameter for continuous NKDE

Jeremy Gelb

2024-05-19

Source: vignettes/web_vignettes/SpeedVSprecision.Rmd

Introduction

In this vignette, we quantify the impact of the parameter max_dept on the precision of the calculation of the continuous NKDE.

The continuous NKDE is obtained by a recursive algorithm correcting the density values along the network when a intersection is encountered. This is the only NKDE that needs to go backward during its calculation and this makes it the slowest approach in terms of computation time.

The parameter max_dept can be used to limit the number of recursions at the cost of a loss in precision. Indeed, at each intersection the density is split in each direction. After a few intersections, it could be considered safe to stop the calculation. The gain in precision is likely not worth the computation time.

In this vignette, we gives some insights about the size of the impact of the parameter max_dept.

We will calculate the impact of the parameter max_dept given several bandwidth for the data bike_accidents.

For each bandwidth, we will recalculate the density with a max_dept value going from 4 to 14. We will then compare the densities obtained with the reference value (highest max_dept). The differences will be summarized with a scaled root mean square error.

\[ SRMSE = \sqrt(\frac{{RMSE}}{\delta}) \] with \(\delta\) equal to the interquartile range for the reference density values.

Preparing the data

We start here by loading the data and preparing the parameters.

# first load data and packages
library(sf)
library(spNetwork)
library(future)
library(future.apply)
library(ggplot2)
library(tmap)
library(dplyr)

data(mtl_network)
data(bike_accidents)

lixels <- lixelize_lines(mtl_network,200,mindist = 50)
samples <- lines_center(lixels)

# we select here the bandwidths for calculation
bws <- seq(200,1000,100)

# we select here the max_dept values
max_depts <- seq(4,14,2)

# we create here the dataframe will all the parameters
params_df <- expand.grid(
  bw = bws,
  max_dept = max_depts
)

# we shuffle the dataframe to make the multicore processing
# balanced
params_df <- params_df[sample(1:nrow(params_df)),]

params_df$index <- 1:nrow(params_df)

items <- split(params_df, 1:nrow(params_df))

We can now start the heavy work. We will use multiprocessing to reduce calculation time.


future::plan(future::multisession(workers=12))

progressr::with_progress({
      p <- progressr::progressor(along = items)
      
      all_densities <- future_lapply(items, function(row) {
        t1 <- system.time({
          values <- nkde(mtl_network,
               events = bike_accidents,
               w = rep(1,nrow(bike_accidents)),
               samples = samples,
               kernel_name = "quartic",
               bw = row$bw, div= "bw",
               adaptive = FALSE,
               method = "continuous", digits = 1, tol = 1,
               max_depth = row$max_dept,
               agg = 10,
               grid_shape = c(1,1),
               verbose=FALSE)
        })
        
        p(sprintf("i=%g", row$index))
        return(list(values, t1[[3]]))
      }, future.packages = c("spNetwork"))
})

Impacts on calculation time

We start here by assessing how much the calculation time is affected by the increase in the bandwidth and the max_depth parameter.


params_df$durations <- sapply(all_densities, function(i){i[[2]]}) / 60

ggplot(params_df) + 
  geom_raster(aes(x = bw, y = max_depth, fill = durations),  size = 2) + 
  geom_text(aes(x = bw, y = max_depth, label = round(durations)), color = 'white') + 
  theme_light() + 
  labs(x = 'bandwidth (m)', y = 'max_depth', fill = 'duration (min)')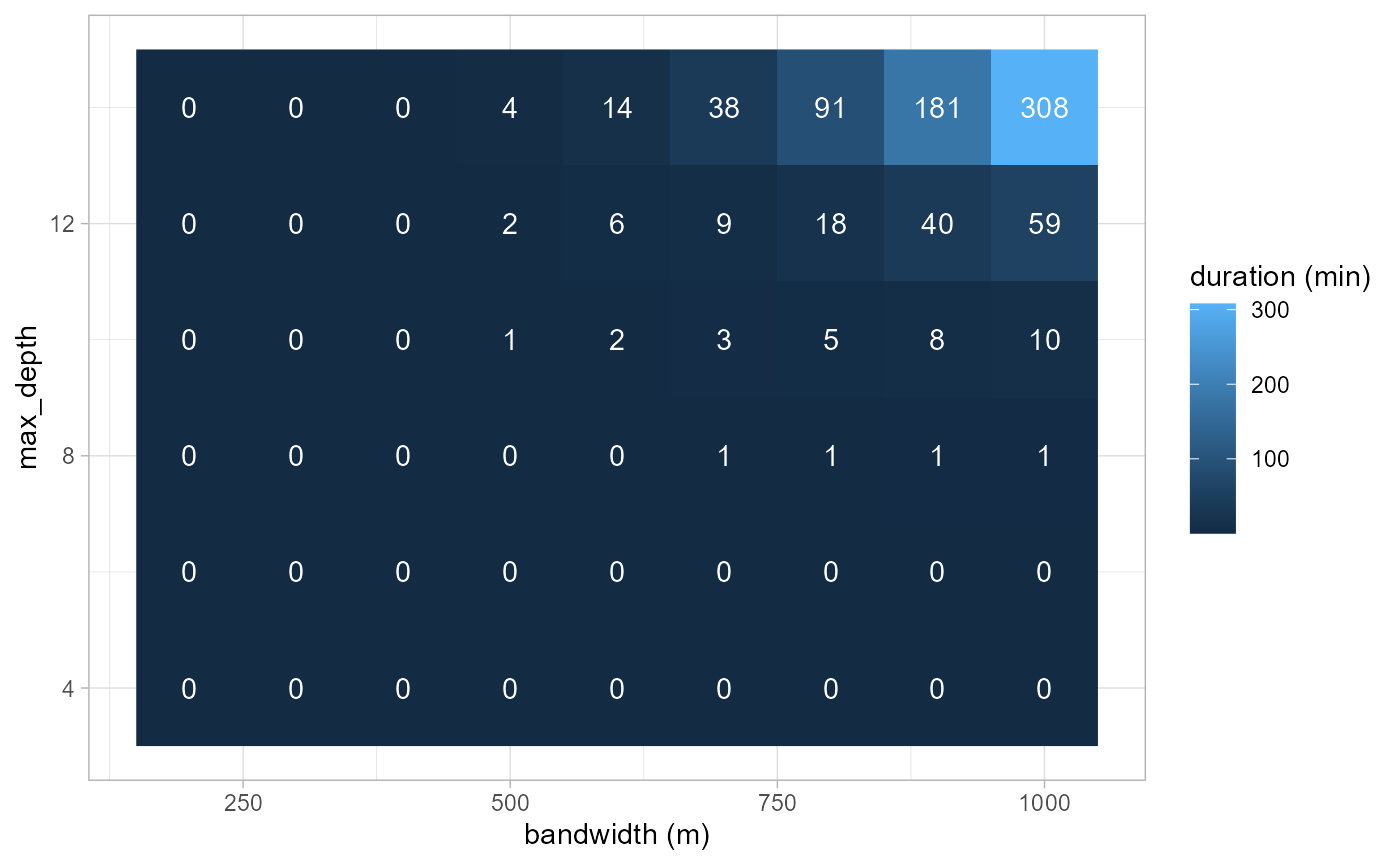

As one can see, the calculation time (in minutes) grows fast with the increasing bandwidth and max_depth. For a small dataset as presented in this vignette and a bandwidth of 1000m, using a max_depth of 8 instead of 10 can divide the calculation time by 10 and by 300 in comparison with the value of 14.

Impact on the results

The reduction in calculation time is very interesting. However, we must check now how much it affects the estimated densities.


references <- subset(params_df, params_df$max_depth == 14)
comparisons <- subset(params_df, params_df$max_depth != 14)

scores <- t(sapply(1:nrow(comparisons), function(i){
  
  row <- comparisons[i,]
  
  idx1 <- row$index
  comp <- all_densities[[idx1]][[1]]
  
  idx2 <- references$index[references$bw == row$bw]
  ref <- all_densities[[idx2]][[1]]
  
  range <- quantile(ref, probs = 0.75) - quantile(ref, probs = 0.25)
  
  error <- sqrt(mean((ref - comp) ** 2)) / range
  
  return(c(row$bw, row$max_dept, error))
  
}))

scores <- data.frame(scores)
names(scores) <- c('bw', 'max_depth', 'error')

ggplot(scores) + 
  geom_raster(aes(x = bw, y = max_depth, fill = error),  size = 2) + 
  geom_text(aes(x = bw, y = max_depth, label = round(error*10,2)), color = 'white') + 
  theme_light() + 
  scale_y_continuous(breaks = unique(comparisons$max_depth)) + 
  scale_x_continuous(breaks = unique(comparisons$bw)) + 
  labs(x = 'bandwidth (m)', y = 'max_depth', fill = 'scaled RMSE')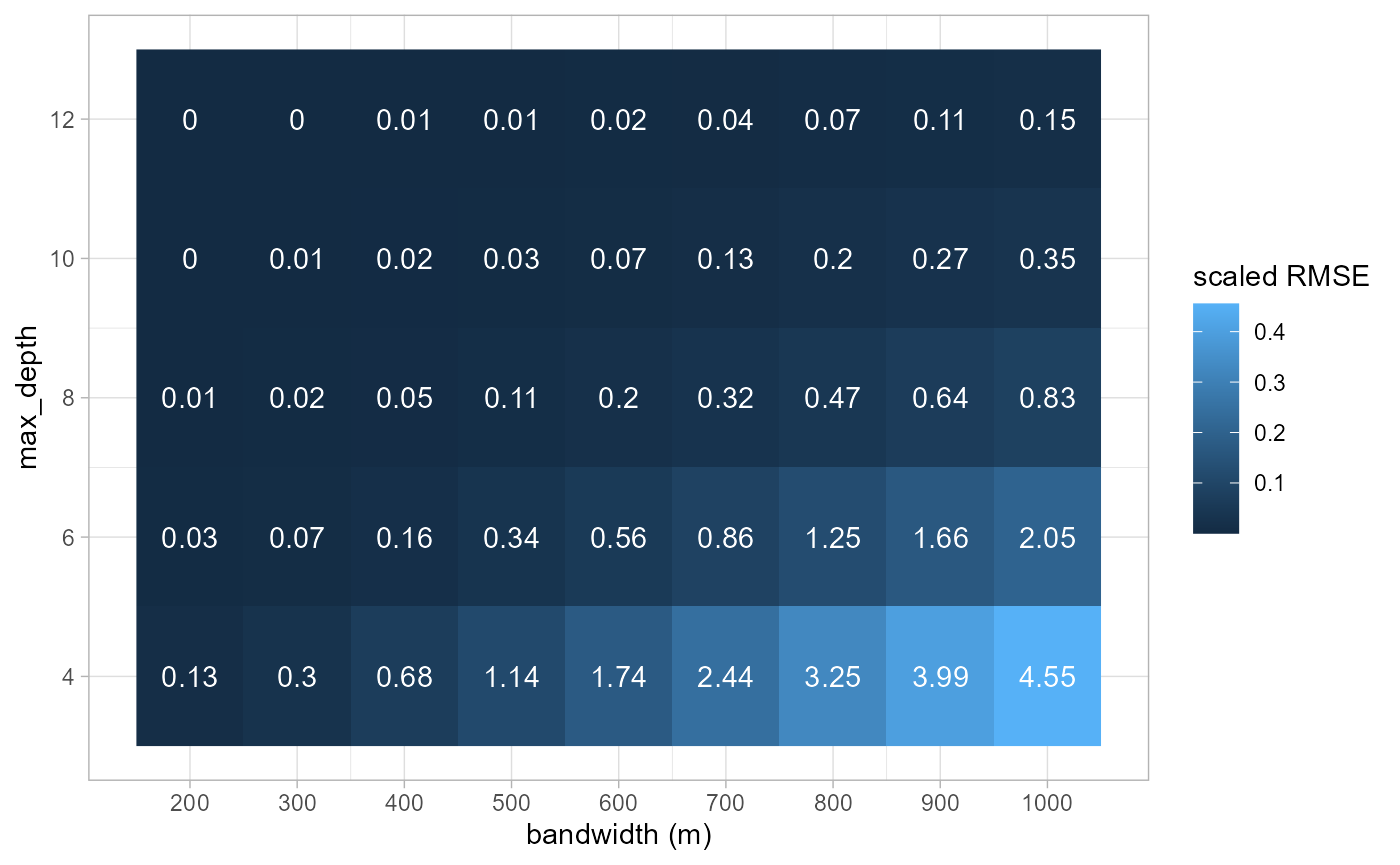

As expected, the scaled RMSE is higher with a larger bandwidth and a smaller max_depth. Considering the link with the bandwidth, we will focus on the results obtained with the largest one (1000m).

To do so, we calculate the relative differences between the reference values (obtained with max_depth = 14) and the approximate values.

ok_ids <- subset(params_df, params_df$bw == 1000 & params_df$max_depth != 14)
reference <- subset(params_df, params_df$bw == 1000 & params_df$max_depth == 14)

ok_ids <- ok_ids[order(ok_ids$max_depth),]

ref <- all_densities[reference$index][[1]]
comparison <- all_densities[ok_ids$index]

plots <- lapply(1:length(comparison), function(i){
  
  df <- data.frame(
    ref = ref[[1]],
    comp = comparison[[i]][[1]],
    diff = (ref[[1]] - comparison[[i]][[1]]) / ref[[1]] * 100
  )
  
  vals <- round(quantile(df$diff, probs = c(0.025, 0.975), na.rm = TRUE))
  
  plot <- ggplot(df) + 
    geom_histogram(aes(x = diff)) + 
    theme_bw() + 
    labs(y = '', x = paste0('max_depth = ',ok_ids$max_depth[[i]]),
         caption = paste0('95% error : ', vals[[1]], '% - ', vals[[2]], '%'))
  
  return(plot)
  
})

ggpubr::ggarrange(plotlist = plots, nrow = 3, ncol = 2)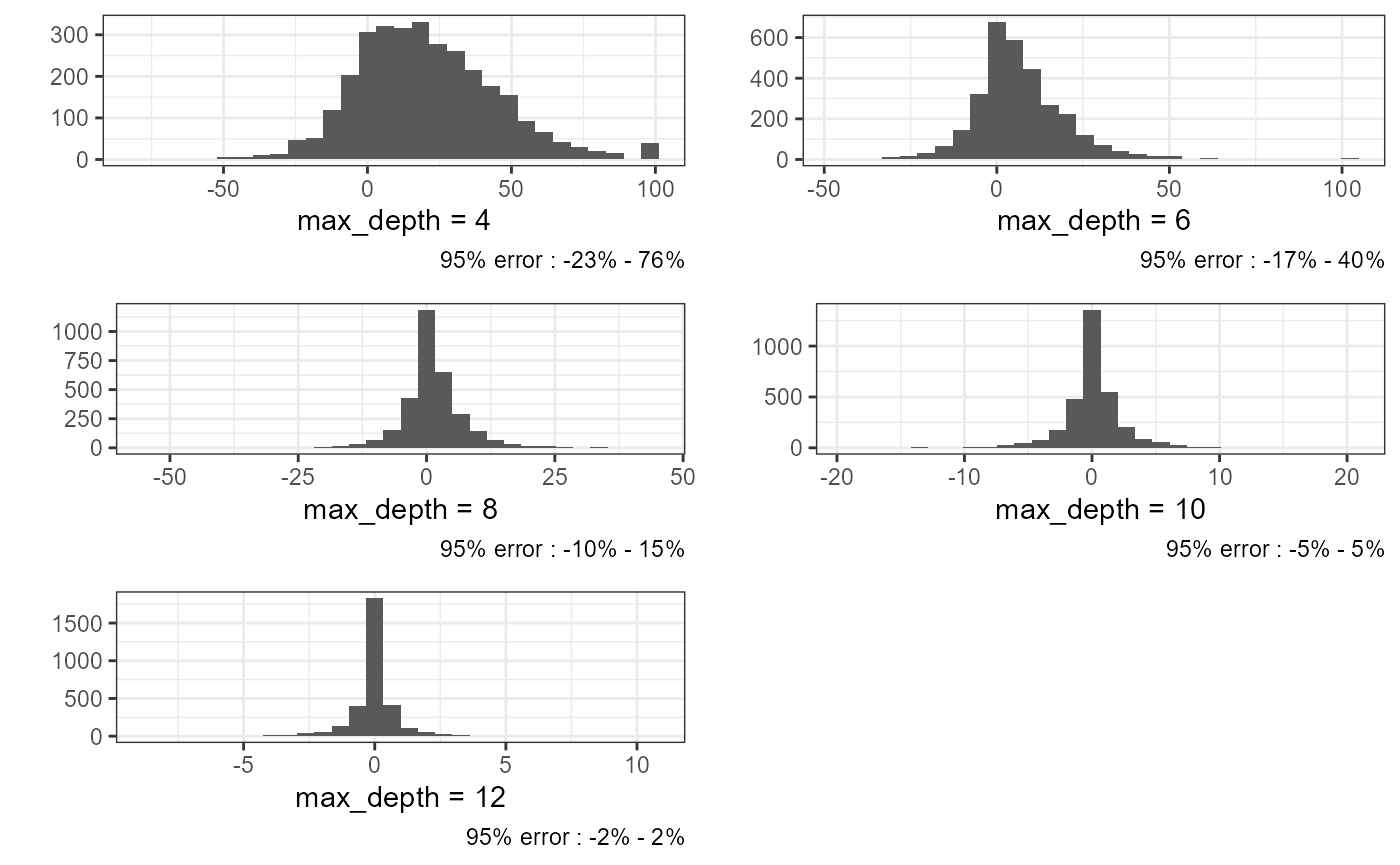

As expected, we can observe a greatest effect when max_depth is very small. With a max_depth at 8, we have 95% of the relative error comprised between -10% and +15% of the local density. On average we can see that the range of the relative error is multiplied by 2.5 each time we decrease the max_depth by two.


plots <- lapply(1:length(comparison), function(i){
  
  df <- data.frame(
    ref = ref[[1]],
    comp = comparison[[i]][[1]],
    diff = (ref[[1]] - comparison[[i]][[1]]) / ref[[1]] * 100
  )
  
  plot <- ggplot(df) + 
    geom_point(aes(x = ref, y = diff)) + 
    labs(x = 'max_depth = 14',
         y = paste0('max_depth = ',ok_ids$max_dept[[i]])
         ) + 
    theme_bw()
  
  return(plot)
  
})

ggpubr::ggarrange(plotlist = plots, nrow = 3, ncol = 2)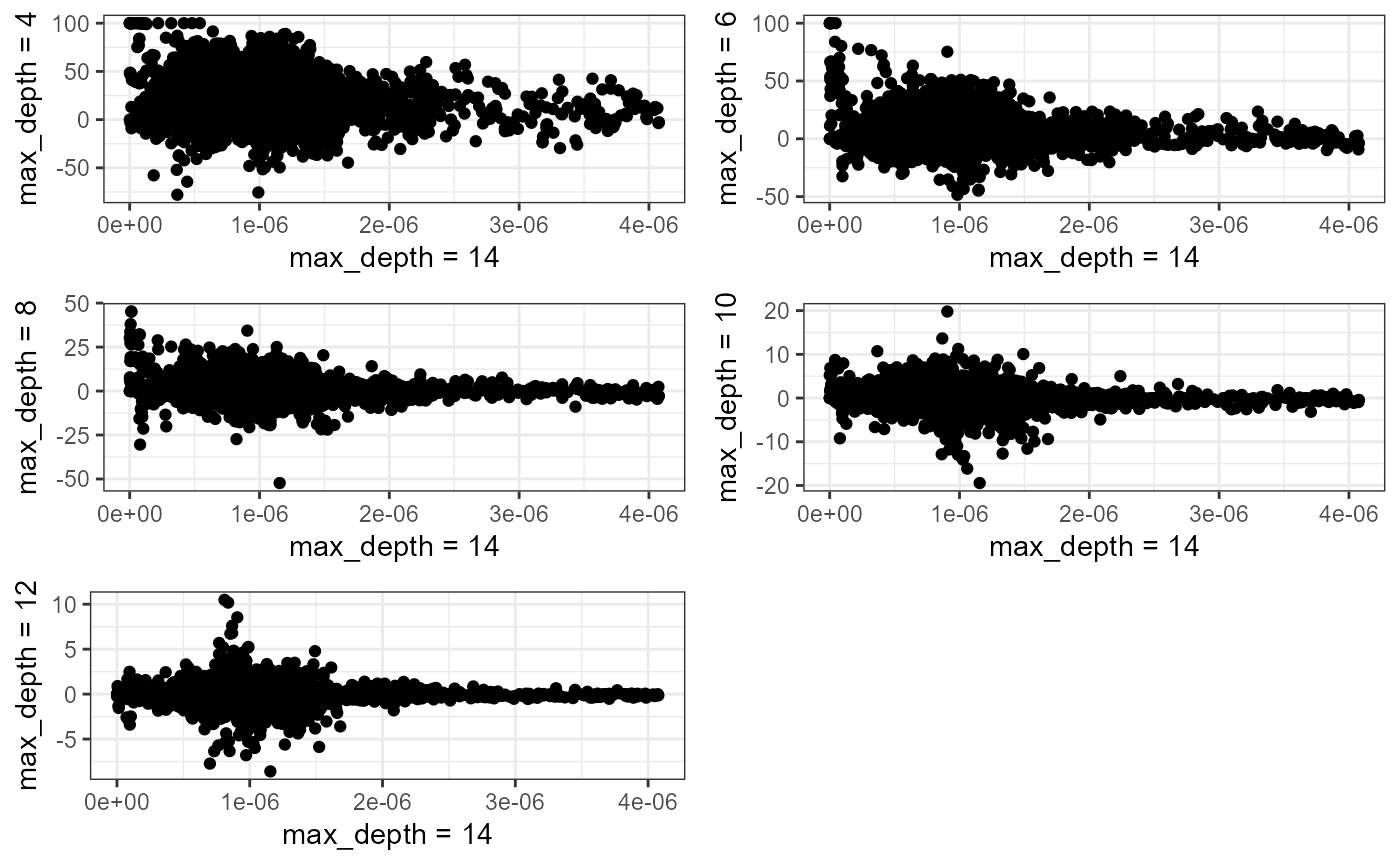

The biggest relative differences are obtained for lixels with low densities. This is not surprising considering the fact that a small change in density leads to a great relative error for lixel with small estimated densities.

lixels$density_14 <- ref[[1]]

id <- ok_ids[ok_ids$max_depth == 10,]$index
lixels$density_10 <- all_densities[[id]][[1]]

lixels$error <- lixels$density_14 - lixels$density_10
lixels$rel_error <- round(lixels$error / lixels$density_14 * 100,1)
lixels$rel_error <- ifelse(is.na(lixels$rel_error), 0, lixels$rel_error)
lixels$rel_error_abs <- abs(lixels$rel_error)

lixels$density_14 <- lixels$density_14 * 1000
lixels$density_10 <- lixels$density_10 * 1000

library(classInt)
library(viridis)

densities <- c(lixels$density_14, lixels$density_10)
color_breaks <- classIntervals(densities, n = 7, style = "kmeans")

map1 <- tm_shape(lixels) + 
  tm_lines('density_14', breaks = color_breaks$brks,
           palette = viridis(7),  title.col = 'density (depth = 14)') + 
  tm_layout(legend.outside = TRUE, frame = FALSE)

map2 <- tm_shape(lixels) + 
  tm_lines('density_10', breaks = color_breaks$brks,
           palette = viridis(7), title.col = 'density (depth = 10)') + 
  tm_layout(legend.outside = TRUE, frame = FALSE)

map3 <- tm_shape(lixels) + 
  tm_lines('rel_error', n = 7, style = 'jenks',
           palette = 'RdBu', title.col = 'relative error (%)') + 
  tm_layout(legend.outside = TRUE, frame = FALSE)

map4 <- tm_shape(lixels) + 
  tm_lines('rel_error_abs', n = 7, style = 'jenks',
           palette = 'Reds', title.col = 'absolute relative error (%)') + 
  tm_layout(legend.outside = TRUE, frame = FALSE)

tmap_arrange(map1, map2, map3, map4)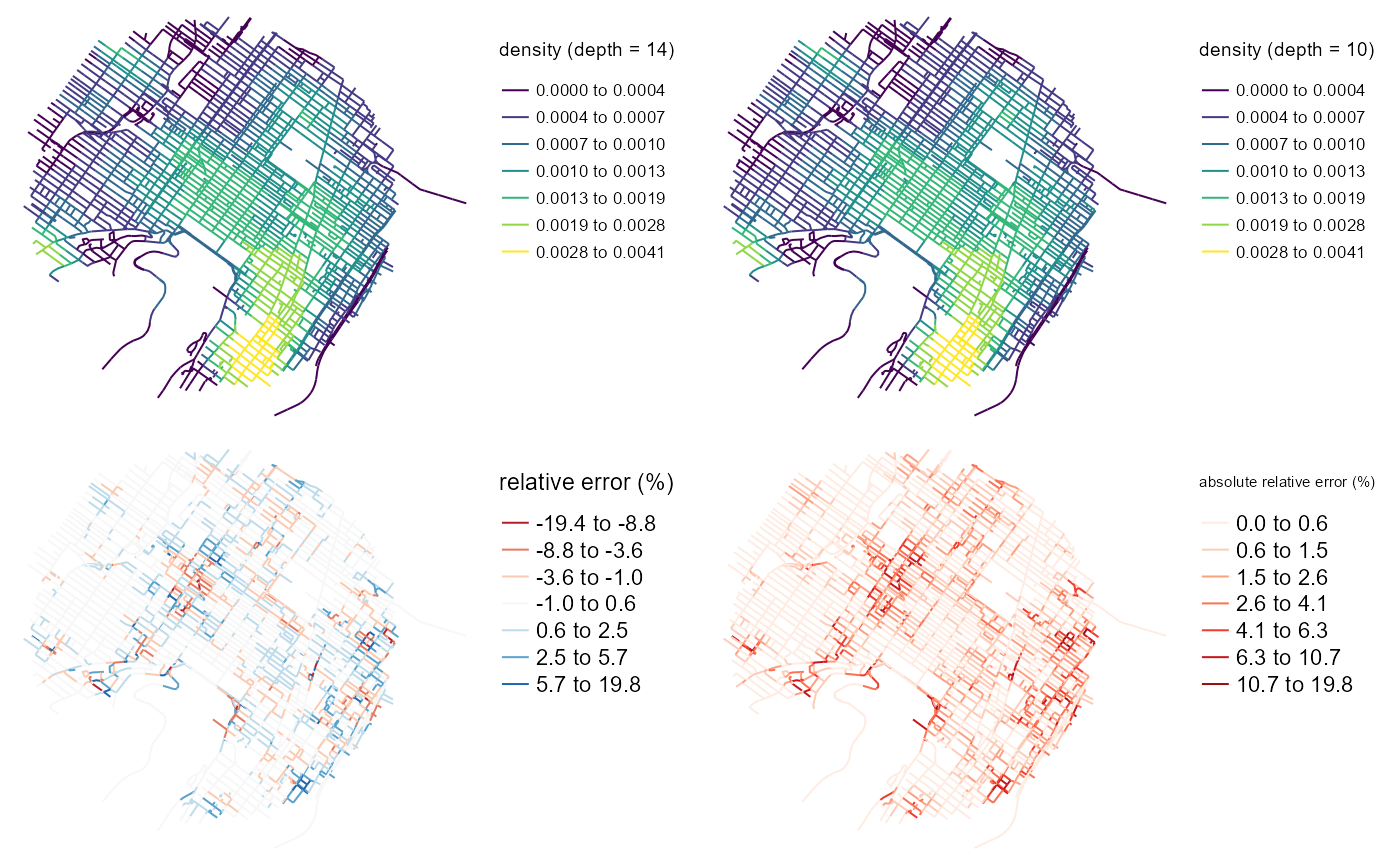

The four maps above show that the error tend to not aggregate at places with high or low densities. This results is important because it suggests that densities and error are not strongly correlated. However, we can see some spatial autocorrelation in the errors.


ok_ids <- subset(params_df, params_df$max_depth != 14)
reference <- subset(params_df, params_df$max_depth == 14)

corr_scores <- t(sapply(1:nrow(ok_ids), function(i){
  
  row <- ok_ids[i,]
  comp <- subset(reference, reference$bw == row$bw)
  dens_ref <- all_densities[[comp$index]][[1]]
  dens_approx <- all_densities[[row$index]][[1]]
  
  error_abs <- abs(dens_ref - dens_approx)
  error <- dens_ref - dens_approx
  return(c(row$bw, row$max_depth,cor(dens_ref, error), cor(dens_ref, error_abs)))
}))

corr_scores <- data.frame(corr_scores)
names(corr_scores) <- c('bw', 'max_depth', 'corr_error', 'corr_abs_error')

corr_scores$max_depth <- as.character(corr_scores$max_depth)
corr_scores <- reshape2::melt(corr_scores, id = c('bw', 'max_depth'))
corr_scores$variable <- as.factor(corr_scores$variable)

ggplot(corr_scores) + 
  geom_point(aes(x = bw, y = value, color = max_depth)) + 
  geom_line(aes(x = bw, y = value, color = max_depth, group = max_depth)) + 
  facet_wrap(vars(variable)) + 
  theme_light()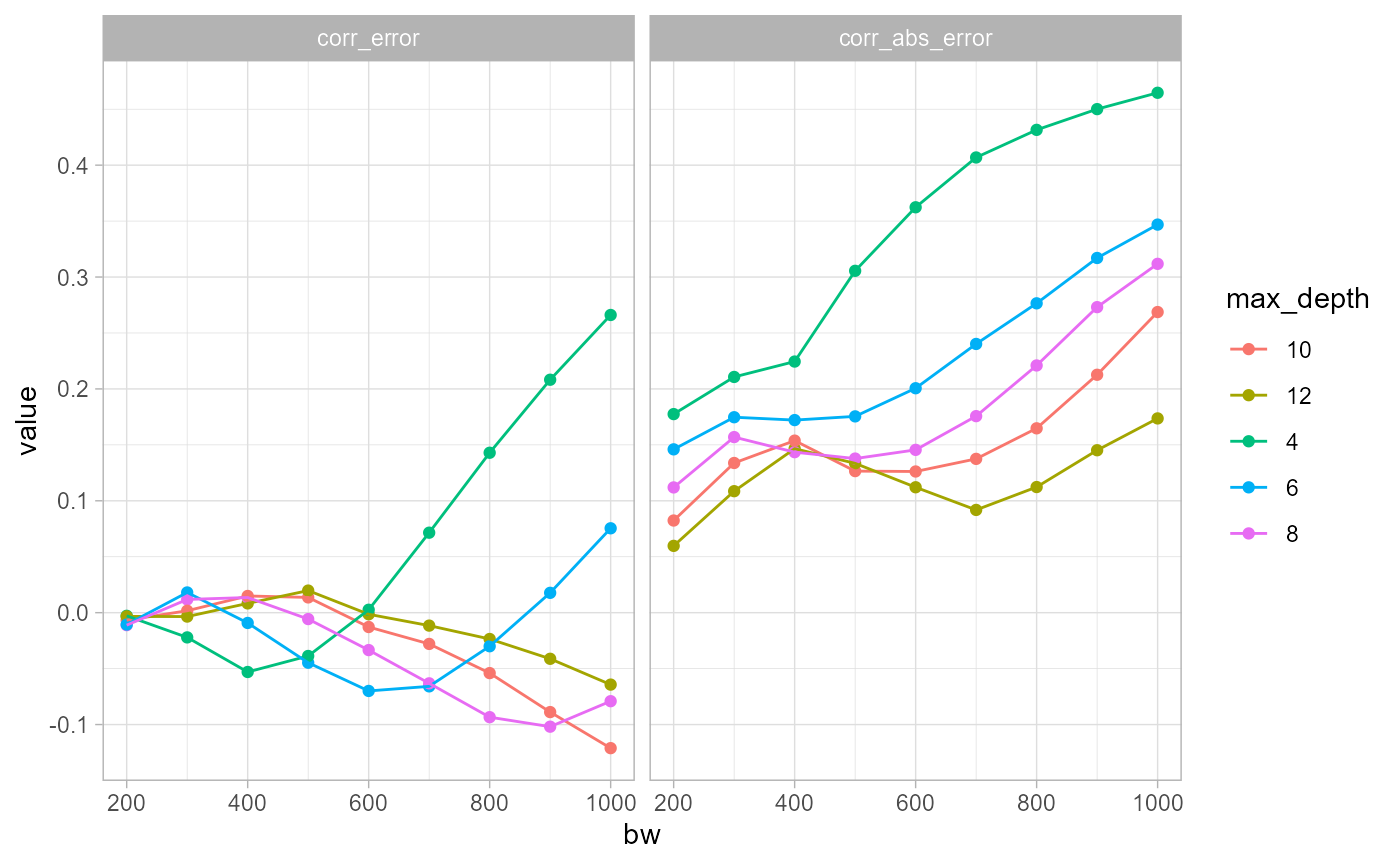

The two plots above illustrate the correlations between the reference density (max_depth = 14) and the error between the approximated density and the reference density. One displays the correlation with the natural error and the second with the absolute error. It is interesting to see that the correlation with the natural error is much greater for small values of max_depth. A value of 8 seems to limit the correlation. In other words, selecting max_depth = 8 can limit greatly the risk that the error caused by simplification is correlated with the real density.

However, the correlations with the absolute errors are all strongly increasing with the bandwidth. This means that at places with higher densities, we might expect higher over or underestimation of the expected density.

Impact on bandwidth selection

Lastly, we want to asses the impact of the max_depth parameter on the bandwidth selection.


items <- c(4,6,8,10,12,14)

df_params2 <- data.frame(
  max_depth = c(4,6,8,10,12,14),
  index = c(1,2,3,4,5,6)
)

items <- split(df_params2, 1:nrow(df_params2))

future::plan(future::multisession(workers=6))

progressr::with_progress({
      p <- progressr::progressor(along = items)
      
      all_bw_scores <- future_lapply(items, function(row) {
        
        values <- bw_cv_likelihood_calc(
            bws = seq(200,1000,50), 
            lines = mtl_network, 
            events = bike_accidents, 
            w = rep(1,nrow(bike_accidents)),
            kernel_name = "quartic", 
            method = 'continuous',
            adaptive = FALSE,
            max_depth = row$max_depth, 
            digits = 1, tol = 1,
            agg = 10,
            grid_shape = c(1,1),
            verbose=FALSE
          )
        
        p(sprintf("i=%g", row$index))
        return(values)
      }, future.packages = c("spNetwork"))
})
all_bw_scores <- do.call(rbind, all_bw_scores)
all_bw_scores$max_depth <- rep(c(4,6,8,10,12,14), each=length(seq(200,1000,50)))

all_bw_scores <- reshape2::melt(all_bw_scores, id = c('bw', 'max_depth'))
all_bw_scores$variable <- as.factor(all_bw_scores$variable)

all_bw_scores$max_depth <- as.character(all_bw_scores$max_depth)

ggplot(all_bw_scores) + 
  geom_point(aes(x = bw, y = value, color = max_depth)) + 
  geom_line(aes(x = bw, y = value, color = max_depth, group = max_depth)) + 
  facet_wrap(vars(variable)) + 
  theme_light()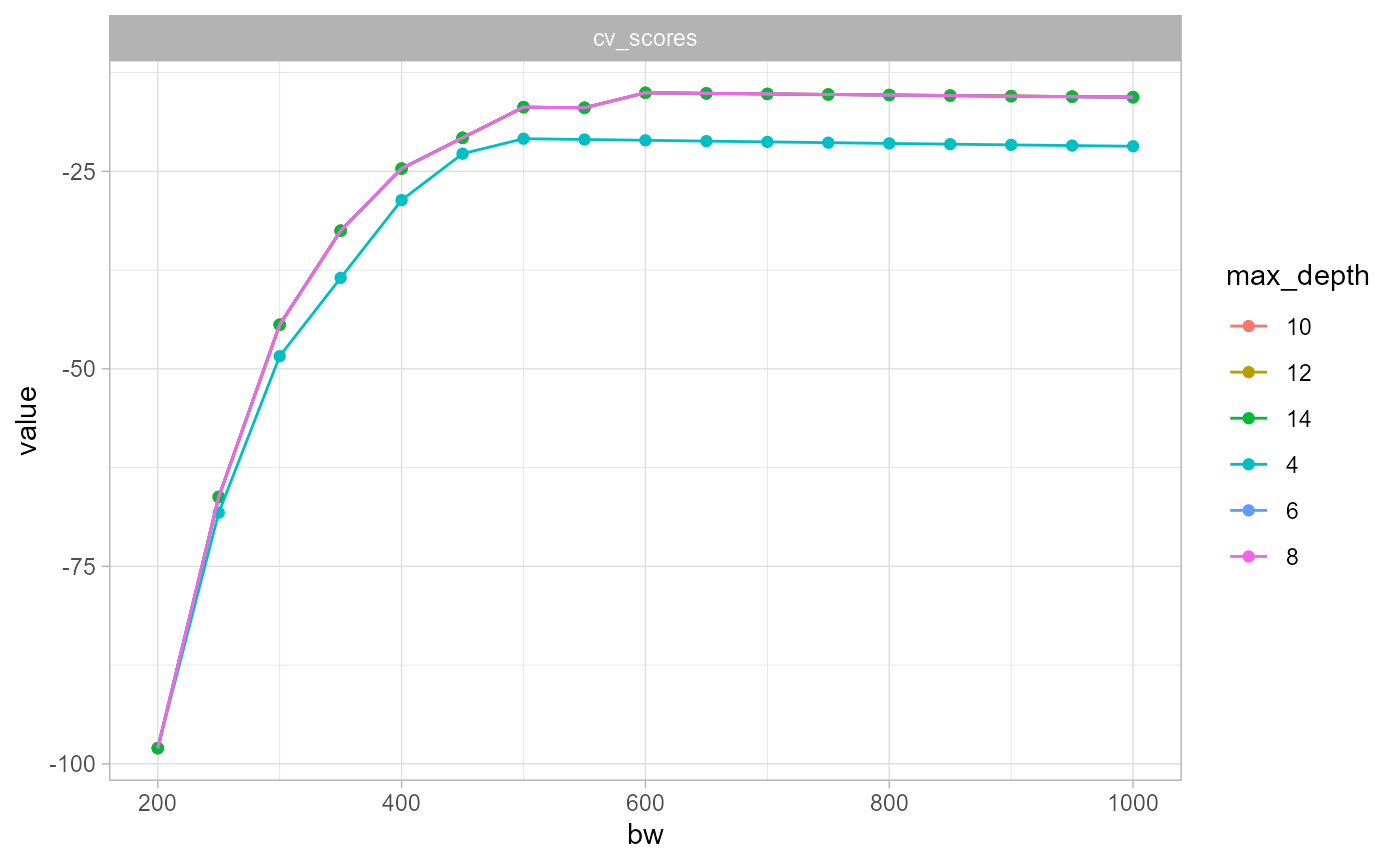

This last results is very interesting. It suggests that the simplification in density calculation affects only marginally the bandwidth selection process.

Final words

Here are the conclusions of this short analysis :

  1. The parameter max_depth can be used to reduce significantly the calculation time.
  2. However, it implies calculating a less accurate estimate of the density value.
  3. The absolute errors are correlated with the local estimates. When the bandwidth increase, the errors thend to be higher were the densities are the highest.
  4. The errors do not affect much the bandwidth selection process. It seems to be safe to use a max_depth of 6 when doing bandwidth selection.